Hi everyone!
I’m excited to share my new NetLogo project: Logônia.
Logônia is a NetLogo model that simulates the growth response of a fictional plant, logônia, under different climatic conditions. The model uses climate data from WorldClim 2.1 and demonstrates how to integrate the LogoClim model through the LevelSpace extension.
The model is openly available on the CoMSES Network and GitHub.
How It Works
Logônia runs on a grid of patches, where each patch represents a piece of soil that can host a plant. Patches correspond to a specific geographic area and store historical climate data for Average Minimum Temperature (°C) (A), Average Maximum Temperature (°C) (B), and Total Precipitation (mm) (C).

Each simulation step represents one month. Over time, plants grow, reproduce, and age. These processes are controlled by sliders on the model’s interface. Climate conditions directly influence growth probability, adding realism and complexity to the simulation.
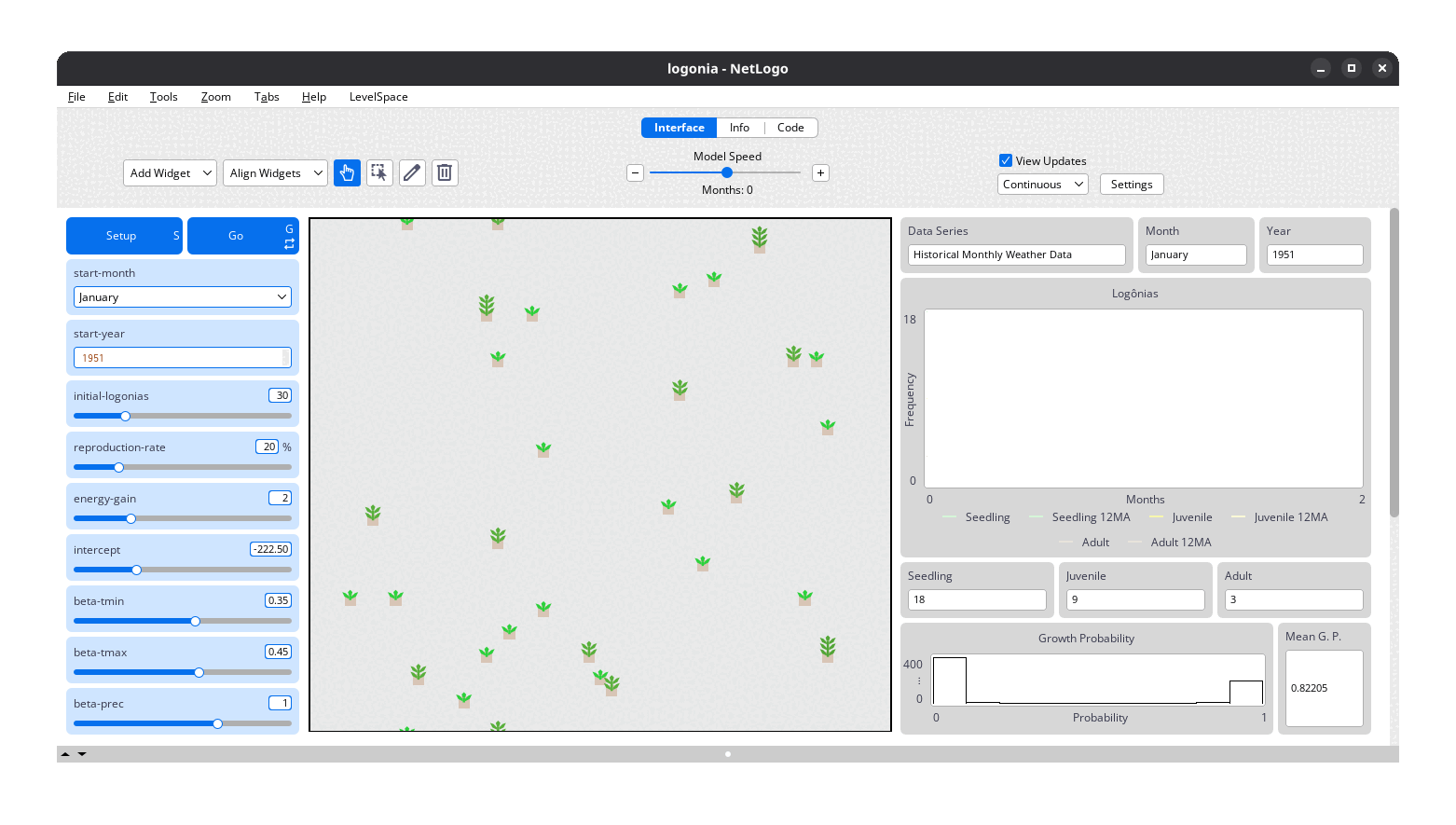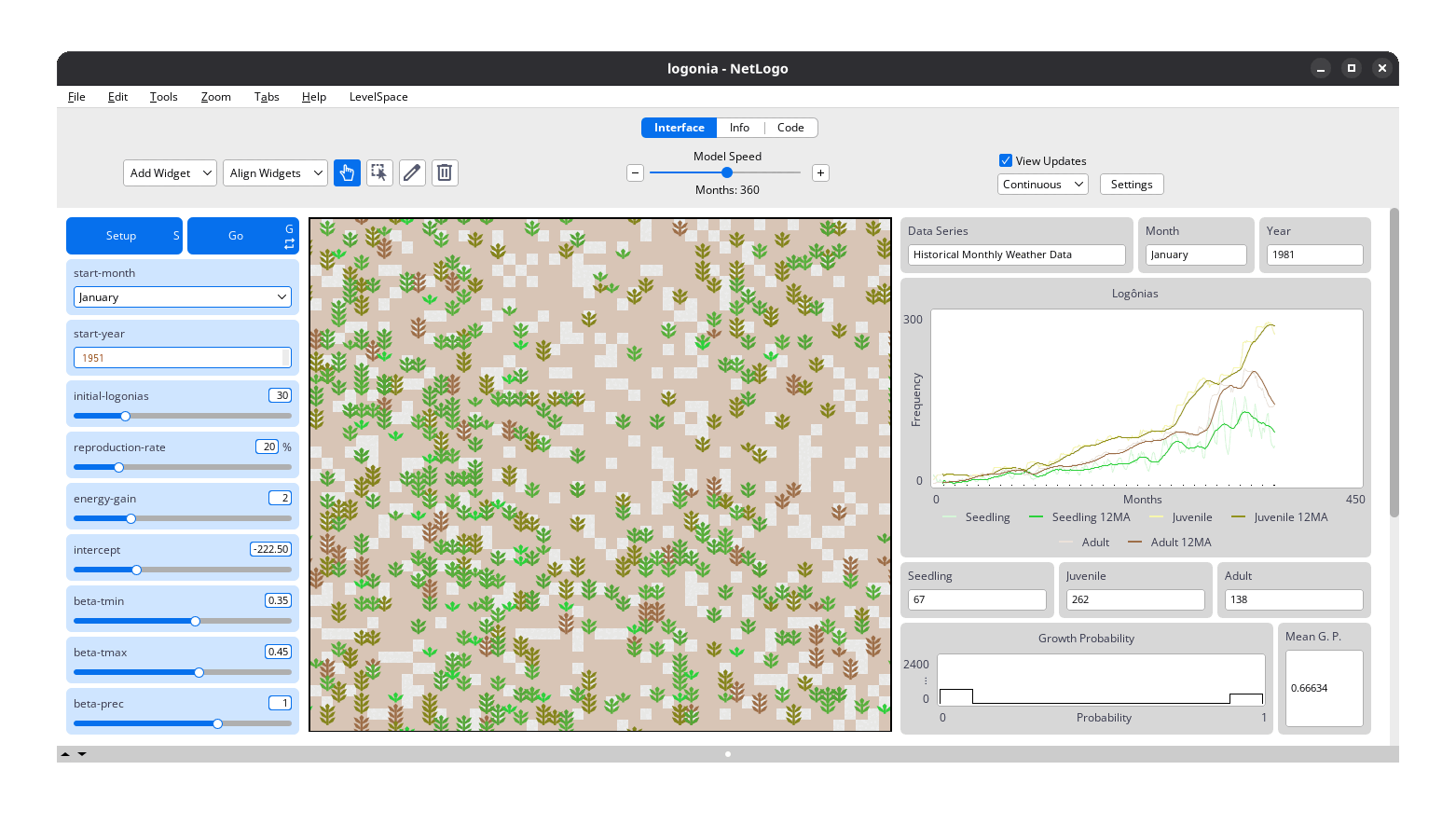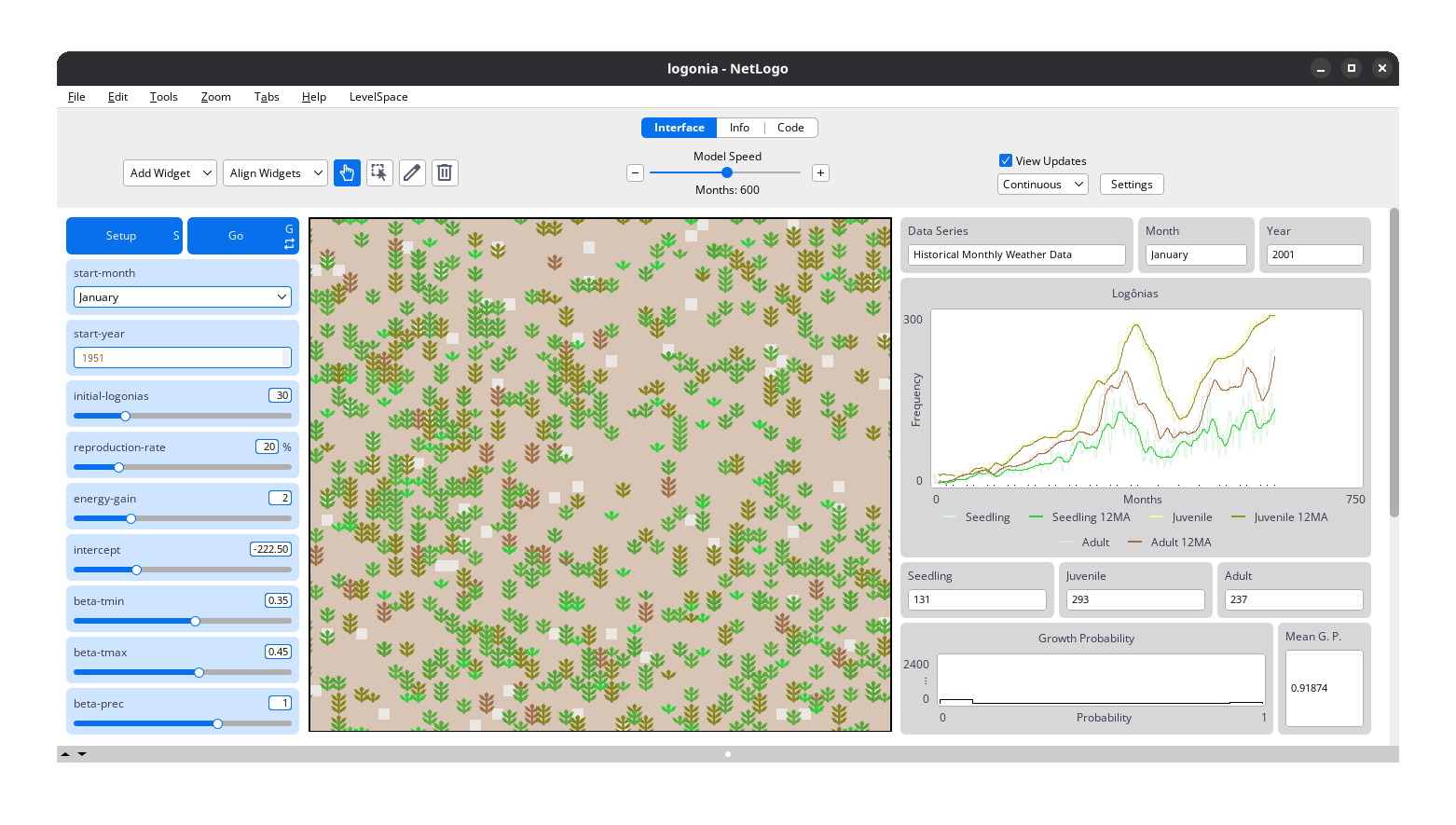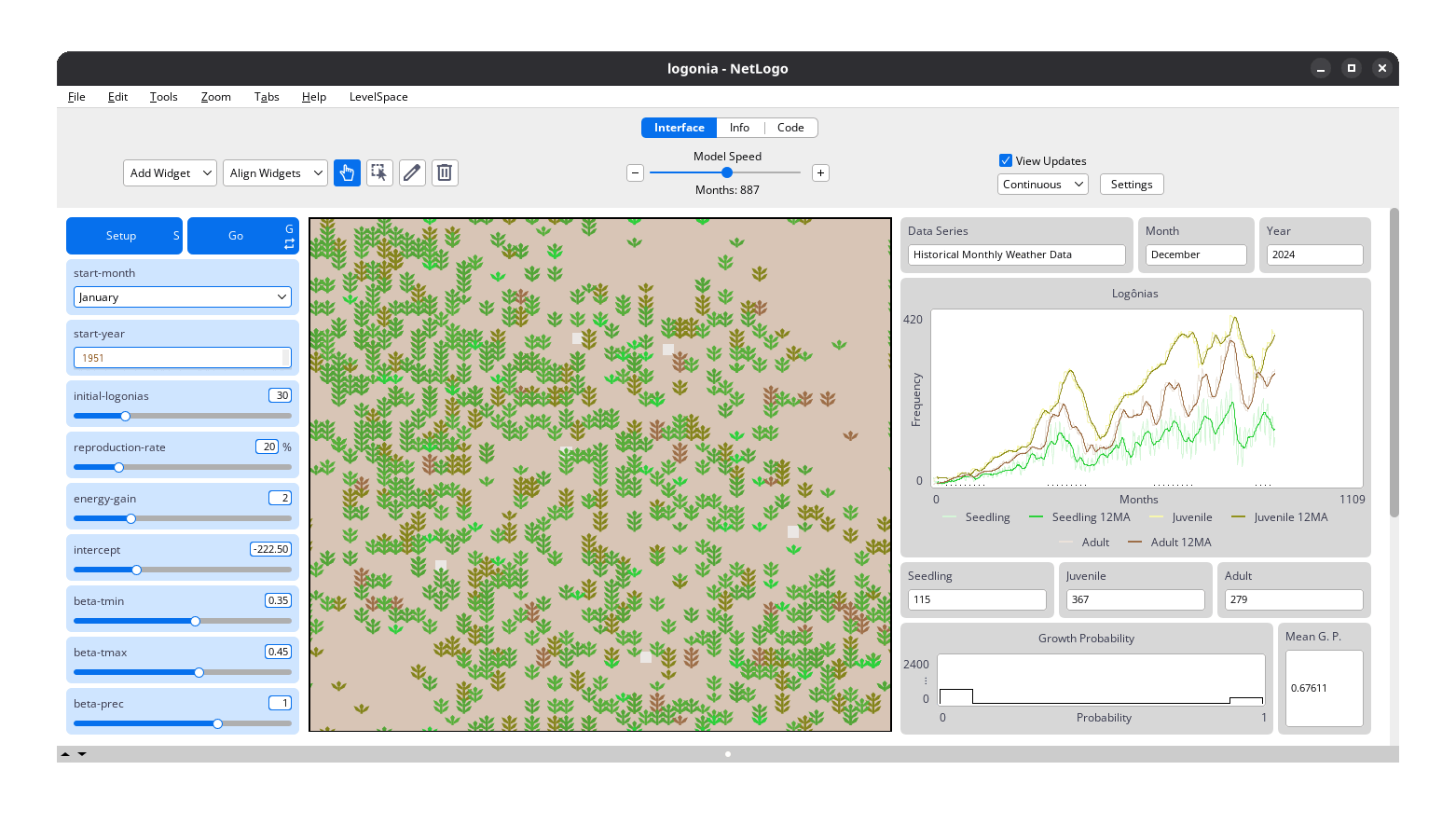
Learn more at: GitHub - sustentarea/logonia: 🌿 Plant Growth Response Model in NetLogo
GitHub Stars are always appreciated! 
Cheers,
Daniel Vartanian
1 Like
Very cool model and use of LevelSpace!
I have one question about the model and then a few smaller notes/questions about the interface.
Question about the model:
You describe the rules of the plant growth as follows:
A logônia gains or loses energy at each step according to the following rules:
- If a random number between
0 and 1 is less than or equal to the growth probability for the current patch, the plant gains the number of energy points defined by the energy-gain slider.
- If the probability is below
0.25 and does not meet the above condition, the plant loses 1 energy point.
- Otherwise, its energy remains unchanged.
Why did you choose to do it this way rather than just drawing the energy gained/lost from a continuous distribution? For example, the variables that currently go into the logistic regression could be used instead to determine the mean of a normal distribution and then each plant draws its energy gained/lost from that distribution. That seems to me like a more natural way to model this, as it could be validated with real data (e.g., grow a bunch of plants under different temperature conditions and measure how much they grow, and then fit growth distributions to the data).
A few notes/questions about the interface:
- For Climate Variable inspection, you only allow inspecting one at at time and if someone sets more than one of
inspect-tmin, inspect-tmax, or inspect-prec to true, you get a message saying only one can be true. Why not just make it a chooser instead of three switches and then you would only be able to select one at at time?
- Why don’t you have
inspection-intercept for inspecting the logistic regression like other variables? Right now, that slider changes the same intercept slider that is used in the real model.
- Why are the value ranges for
intercept, beta-tmin, beta-tmax, beta-prec different from the inspection versions?
Hi @jzkelter,
I’m glad you like the model!
Regarding your question:
That’s a solid idea—I had considered it before, but at the time I felt the model was already complex enough. I might implement it in the future (this suggestion is noted in this issue). Although, I think it would work better if the logistic function parameters could vary slightly for each plant. The challenge with using a normal distribution in simulations is that it’s unbounded.
About your notes/questions on the interface:
- Good point! I’ve already made those changes in the developer version. Thanks for the suggestion!

- The
intercept in the Logistic Regression Inspection section is the same as the intercept slider in the main controls, since beta-tmin, beta-tmax, and beta-prec remain unchanged. This section allows inspecting how the logistic regression behaves across different dimensions (tmin, tmax, and prec). Because the intercept has an additive effect—shifting the sigmoid curve along the x-axis—it felt important to include it here.
- As mentioned in point 2, the ranges differ because they represent different things. The probability equation is:
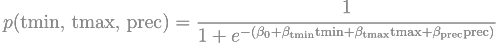
Here, beta-tmin, beta-tmax, and beta-prec are the regression coefficients, while tmin, tmax, and prec are the climate variables.
Thanks again for your thoughtful suggestions—they really help improve the model! Looking forward to hearing any other ideas you might have.
I didn’t look carefully enought at the logistic equation to realize that there are four contants and three variables. Makes sense!
I still don’t understand why you would prefer a logistic function. There are plenty of alternatives to a normal distribution which are bounded. Is there a way you could take real data on plant growth, t_min, t_max, and precipitation and use it to fit the parameters of the logistic function to it? I don’t see how you could, given that it only gives you a probability of growth, not an amount of growth, but I’m not an expert in statistical models.


![]()